What Are the Solutions to the Quadratic Equation (5y 6)2 = 24?

Quadratic Equations

83 Solve Quadratic Equations Using the Quadratic Formula

Learning Objectives

By the finish of this section, you will be able to:

Solve quadratic equations using the quadratic formula
Utilize the discriminant to predict the number of solutions of a quadratic equation
Identify the most appropriate method to use to solve a quadratic equation

When we solved quadratic equations in the last section by completing the foursquare, we took the same steps every time. By the end of the exercise set, you may have been wondering 'isn't at that place an easier way to do this?' The answer is 'yes.' In this department, we will derive and utilize a formula to find the solution of a quadratic equation.

We have already seen how to solve a formula for a specific variable 'in general' and so that nosotros would exercise the algebraic steps but once and and so use the new formula to find the value of the specific variable. At present, we will become through the steps of completing the square in full general to solve a quadratic equation for x. It may be helpful to wait at one of the examples at the terminate of the last section where we solved an equation of the form $a{x}^{2}+bx+c=0$ as you read through the algebraic steps below, so you run into them with numbers equally well equally 'in general.'

$\begin{array}{cccccc}\text{We start with the standard form of a quadratic equation}\hfill & & & \hfill a{x}^{2}+bx+c& =\hfill & 0\phantom{\rule{2em}{0ex}}a\ne 0\hfill \\ \text{and solve it for}\phantom{\rule{0.2em}{0ex}}x\phantom{\rule{0.2em}{0ex}}\text{by completing the square.}\hfill & & & & & \\ \text{Isolate the variable terms on one side.}\hfill & & & \hfill a{x}^{2}+bx& =\hfill & \text{−}c\hfill \\ \\ \\ \text{Make leading coefficient 1, by dividing by a.}\hfill & & & \hfill \frac{a{x}^{2}}{a}+\frac{b}{a}x& =\hfill & -\frac{c}{a}\hfill \\ \\ \\ \text{Simplify.}\hfill & & & \hfill {x}^{2}+\frac{b}{a}x& =\hfill & -\frac{c}{a}\hfill \\ \text{To complete the square, find}\phantom{\rule{0.2em}{0ex}}{\left(\frac{1}{2}·\frac{b}{a}\right)}^{2}\phantom{\rule{0.2em}{0ex}}\text{and add it to both}\hfill & & & \\ \text{sides of the equation.}\phantom{\rule{0.2em}{0ex}}{\left(\frac{1}{2}\phantom{\rule{0.2em}{0ex}}\frac{b}{a}\right)}^{2}=\frac{{b}^{2}}{4{a}^{2}}\hfill & & & \hfill {x}^{2}+\frac{b}{a}x+\frac{{b}^{2}}{4{a}^{2}}& =\hfill & -\frac{c}{a}+\frac{{b}^{2}}{4{a}^{2}}\hfill \\ \\ \\ \text{The left side is a perfect square, factor it.}\hfill & & & \hfill {\left(x+\frac{b}{2a}\right)}^{2}& =\hfill & -\frac{c}{a}+\frac{{b}^{2}}{4{a}^{2}}\hfill \\ \\ \\ \begin{array}{c}\text{Find the common denominator of the right side and write}\hfill \\ \text{equivalent fractions with the common denominator.}\hfill \end{array}\hfill & & & \hfill {\left(x+\frac{b}{2a}\right)}^{2}& =\hfill & \frac{{b}^{2}}{4{a}^{2}}-\frac{c·4a}{a·4a}\hfill \\ \\ \\ \text{Simplify.}\hfill & & & \hfill {\left(x+\frac{b}{2a}\right)}^{2}& =\hfill & \frac{{b}^{2}}{4{a}^{2}}-\frac{4ac}{4{a}^{2}}\hfill \\ \\ \\ \text{Combine to one fraction.}\hfill & & & \hfill {\left(x+\frac{b}{2a}\right)}^{2}& =\hfill & \frac{{b}^{2}-4ac}{4{a}^{2}}\hfill \\ \\ \\ \text{Use the square root property.}\hfill & & & \hfill x+\frac{b}{2a}& =\hfill & ±\phantom{\rule{0.2em}{0ex}}\sqrt{\frac{{b}^{2}-4ac}{4{a}^{2}}}\hfill \\ \\ \\ \text{Simplify.}\hfill & & & \hfill x+\frac{b}{2a}& =\hfill & ±\phantom{\rule{0.2em}{0ex}}\frac{\sqrt{{b}^{2}-4ac}}{2a}\hfill \\ \\ \\ \text{Add}\phantom{\rule{0.2em}{0ex}}-\frac{b}{2a}\phantom{\rule{0.2em}{0ex}}\text{to both sides of the equation.}\hfill & & & \hfill x& =\hfill & -\frac{b}{2a}±\frac{\sqrt{{b}^{2}-4ac}}{2a}\hfill \\ \\ \\ \text{Combine the terms on the right side.}\hfill & & & \hfill x& =\hfill & \frac{\text{−}b±\sqrt{{b}^{2}-4ac}}{2a}\hfill \end{array}$

This last equation is the Quadratic Formula.

Quadratic Formula

The solutions to a quadratic equation of the form $a{x}^{2}+bx+c=0$ , $a\ne 0$ are given by the formula:

$x=\frac{\text{−}b±\sqrt{{b}^{2}-4ac}}{2a}$

To use the Quadratic Formula, we substitute the values of $a,b,\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}c$ into the expression on the correct side of the formula. Then, nosotros exercise all the math to simplify the expression. The result gives the solution(s) to the quadratic equation.

How to Solve a Quadratic Equation Using the Quadratic Formula

Solve $2{x}^{2}+9x-5=0$ by using the Quadratic Formula.

Solve $3{y}^{2}-5y+2=0$ past using the Quadratic Formula.

$y=\frac{2}{3},y=1$

Solve $4{z}^{2}+2z-6=0$ by using the Quadratic Formula.

$z=-\frac{3}{2},z=1$

If you say the formula equally you write it in each trouble, you'll have it memorized in no time. And remember, the Quadratic Formula is an equation. Be sure you first with ' $x=$ '.

Solve ${x}^{2}-6x+5=0$ by using the Quadratic Formula.

Solve ${a}^{2}-2a-15=0$ past using the Quadratic Formula.

$a=-3,a=5$

Solve ${b}^{2}+10b+24=0$ by using the Quadratic Formula.

$b=-6,b=-4$

When we solved quadratic equations by using the Square Root Property, we sometimes got answers that had radicals. That tin can happen, likewise, when using the Quadratic Formula. If we get a radical every bit a solution, the terminal respond must have the radical in its simplified form.

Solve $4{y}^{2}-5y-3=0$ by using the Quadratic Formula.

Solve $2{p}^{2}+8p+5=0$ by using the Quadratic Formula.

$p=\frac{-4±\sqrt{6}}{2}$

Solve $5{q}^{2}-11q+3=0$ by using the Quadratic Formula.

$q=\frac{11±\sqrt{61}}{10}$

Solve $2{x}^{2}+10x+11=0$ by using the Quadratic Formula.

Solve $3{m}^{2}+12m+7=0$ past using the Quadratic Formula.

$m=\frac{-6±\sqrt{15}}{3}$

Solve $5{n}^{2}+4n-4=0$ by using the Quadratic Formula.

$n=\frac{-2±2\sqrt{6}}{5}$

We cannot accept the foursquare root of a negative number. Then, when we substitute $a$ , $b$ , and $c$ into the Quadratic Formula, if the quantity inside the radical is negative, the quadratic equation has no existent solution. We will see this in the side by side example.

Solve $3{p}^{2}+2p+9=0$ by using the Quadratic Formula.

Solve $4{a}^{2}-3a+8=0$ by using the Quadratic Formula.

no real solution

Solve $5{b}^{2}+2b+4=0$ past using the Quadratic Formula.

no existent solution

The quadratic equations we take solved so far in this section were all written in standard form, $a{x}^{2}+bx+c=0$ . Sometimes, we will need to exercise some algebra to get the equation into standard form before we can utilise the Quadratic Formula.

Solve $x\left(x+6\right)+4=0$ by using the Quadratic Formula.

Solve $x\left(x+2\right)-5=0$ by using the Quadratic Formula.

$x=-1±\sqrt{6}$

Solve $y\left(3y-1\right)-2=0$ by using the Quadratic Formula.

$y=-\frac{2}{3},y=1$

When we solved linear equations, if an equation had besides many fractions we 'cleared the fractions' by multiplying both sides of the equation by the LCD. This gave us an equivalent equation—without fractions—to solve. We can apply the same strategy with quadratic equations.

Solve $\frac{1}{2}{u}^{2}+\frac{2}{3}u=\frac{1}{3}$ by using the Quadratic Formula.

Solve $\frac{1}{4}{c}^{2}-\frac{1}{3}c=\frac{1}{12}$ by using the Quadratic Formula.

$c=\frac{2±\sqrt{7}}{3}$

Solve $\frac{1}{9}{d}^{2}-\frac{1}{2}d=-\frac{1}{2}$ by using the Quadratic Formula.

$d=\frac{2}{3},d=0$

Recollect about the equation ${\left(x-3\right)}^{2}=0$ . We know from the Zero Products Principle that this equation has but ane solution: $x=3$ .

We will encounter in the next example how using the Quadratic Formula to solve an equation with a perfect foursquare also gives merely one solution.

Solve $4{x}^{2}-20x=-25$ by using the Quadratic Formula.

Solve ${r}^{2}+10r+25=0$ by using the Quadratic Formula.

$r=-5$

Solve $25{t}^{2}-40t=-16$ by using the Quadratic Formula.

$t=\frac{4}{5}$

Use the Discriminant to Predict the Number of Solutions of a Quadratic Equation

When we solved the quadratic equations in the previous examples, sometimes we got two solutions, sometimes one solution, sometimes no existent solutions. Is in that location a manner to predict the number of solutions to a quadratic equation without actually solving the equation?

Aye, the quantity inside the radical of the Quadratic Formula makes it easy for us to make up one's mind the number of solutions. This quantity is called the discriminant.

Discriminant

In the Quadratic Formula $x=\frac{\text{−}b±\sqrt{{b}^{2}-4ac}}{2a}$ , the quantity ${b}^{2}-4ac$ is called the discriminant.

Let'due south wait at the discriminant of the equations in (Figure), (Figure), and (Figure), and the number of solutions to those quadratic equations.

	Quadratic Equation (in standard form)	Discriminant ${b}^{2}-4ac$	Sign of the Discriminant	Number of real solutions
(Effigy)	$2{x}^{2}+9x-5=0$	${9}^{2}-4·2\left(-5\right)=121$	+	2
(Figure)	$4{x}^{2}-20x+25=0$	${\left(-20\right)}^{2}-4·4·25=0$	0	1
(Figure)	$3{p}^{2}+2p+9=0$	${2}^{2}-4·3·9=-104$	−	0

When the discriminant is positive $\left(x=\frac{\text{−}b±\sqrt{+}}{2a}\right)$ the quadratic equation has two solutions.

When the discriminant is naught $\left(x=\frac{\text{−}b±\sqrt{0}}{2a}\right)$ the quadratic equation has i solution.

When the discriminant is negative $\left(x=\frac{\text{−}b±\sqrt{-}}{2a}\right)$ the quadratic equation has no real solutions.

Use the discriminant, ${b}^{2}-4ac$ , to determine the number of solutions of a Quadratic Equation.

For a quadratic equation of the form $a{x}^{2}+bx+c=0$ , $a\ne 0$ ,

Decide the number of solutions to each quadratic equation:

ⓐ $2{v}^{2}-3v+6=0$ ⓑ $3{x}^{2}+7x-9=0$ ⓒ $5{n}^{2}+n+4=0$ ⓓ $9{y}^{2}-6y+1=0$

Solution

To determine the number of solutions of each quadratic equation, nosotros will look at its discriminant.

ⓐ
$\begin{array}{cccc}& & & \hfill \phantom{\rule{5em}{0ex}}2{v}^{2}-3v+6=0\\ \text{The equation is in standard form, identify}\phantom{\rule{0.2em}{0ex}}a,b,c.\hfill & & & \hfill \phantom{\rule{5em}{0ex}}a=2,b=-3,c=6\\ \text{Write the discriminant.}\hfill & & & \hfill \phantom{\rule{5em}{0ex}}{b}^{2}-4ac\phantom{\rule{1.3em}{0ex}}\\ \text{Substitute in the values of}\phantom{\rule{0.2em}{0ex}}a,b,c.\hfill & & & \hfill \phantom{\rule{5em}{0ex}}{\left(3\right)}^{2}-4·2·6\\ \text{Simplify.}\hfill & & & \hfill \phantom{\rule{5em}{0ex}}\begin{array}{c}\hfill 9-48\phantom{\rule{1.7em}{0ex}}\\ \hfill -39\phantom{\rule{2.1em}{0ex}}\end{array}\\ \text{Because the discriminant is negative, there are no real}\hfill & & & \\ \text{solutions to the equation.}\hfill & & & \end{array}$
ⓑ
$\begin{array}{cccc}& & & \hfill \phantom{\rule{6.2em}{0ex}}3{x}^{2}+7x-9=0\\ \text{The equation is in standard form, identify}\phantom{\rule{0.2em}{0ex}}a,b,c.\hfill & & & \hfill \phantom{\rule{6.2em}{0ex}}a=3,b=7,c=-9\\ \text{Write the discriminant.}\hfill & & & \hfill \phantom{\rule{6.2em}{0ex}}{b}^{2}-4ac\phantom{\rule{2.6em}{0ex}}\\ \text{Substitute in the values of}\phantom{\rule{0.2em}{0ex}}a,b,c.\hfill & & & \hfill \phantom{\rule{6.2em}{0ex}}{\left(7\right)}^{2}-4·3·\left(-9\right)\\ \text{Simplify.}\hfill & & & \hfill \phantom{\rule{6.2em}{0ex}}\begin{array}{c}\hfill 49+108\phantom{\rule{2.6em}{0ex}}\\ \hfill 157\phantom{\rule{3.4em}{0ex}}\end{array}\\ \text{Because the discriminant is positive, there are two}\hfill & & & \\ \text{solutions to the equation.}\hfill & & & \end{array}$
ⓒ
$\begin{array}{cccc}& & & \hfill \phantom{\rule{5em}{0ex}}5{n}^{2}+n+4=0\\ \text{The equation is in standard form, identify}\phantom{\rule{0.2em}{0ex}}a,b,\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}c.\hfill & & & \hfill \phantom{\rule{5em}{0ex}}a=5,b=1,c=4\\ \text{Write the discriminant.}\hfill & & & \hfill \phantom{\rule{5em}{0ex}}{b}^{2}-4ac\phantom{\rule{1.2em}{0ex}}\\ \text{Substitute in the values of}\phantom{\rule{0.2em}{0ex}}a,b,c.\hfill & & & \hfill \phantom{\rule{5em}{0ex}}{\left(1\right)}^{2}-4·5·4\\ \text{Simplify.}\hfill & & & \hfill \phantom{\rule{5em}{0ex}}\begin{array}{c}\hfill 1-80\phantom{\rule{1.7em}{0ex}}\\ \hfill -79\phantom{\rule{2.1em}{0ex}}\end{array}\\ \text{Because the discriminant is negative, there are no real}\hfill & & & \\ \text{solutions to the equation.}\hfill & & & \end{array}$
ⓓ
$\begin{array}{cccc}& & & \hfill 9{y}^{2}-6y+1=0\\ \text{The equation is in standard form, identify}\phantom{\rule{0.2em}{0ex}}a,b,c.\hfill & & & \hfill a=9,b=-6,c=1\\ \text{Write the discriminant.}\hfill & & & \hfill {b}^{2}-4ac\phantom{\rule{1.2em}{0ex}}\\ \text{Substitute in the values of}\phantom{\rule{0.2em}{0ex}}a,b,c.\hfill & & & \hfill {\left(-6\right)}^{2}-4·9·1\\ \text{Simplify.}\hfill & & & \hfill \begin{array}{c}\hfill 36-36\phantom{\rule{1.6em}{0ex}}\\ \hfill 0\phantom{\rule{2.7em}{0ex}}\end{array}\\ \text{Because the discriminant is 0, there is one solution to the equation.}\hfill & & & \end{array}$

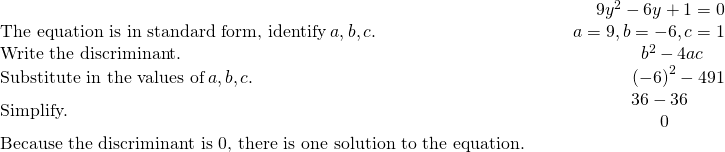
Determine the number of solutions to each quadratic equation:

ⓐ $8{m}^{2}-3m+6=0$ ⓑ $5{z}^{2}+6z-2=0$ ⓒ $9{w}^{2}+24w+16=0$ ⓓ $9{u}^{2}-2u+4=0$

ⓐ no real solutions ⓑ 2 ⓒ 1 ⓓ no real solutions

Determine the number of solutions to each quadratic equation:

ⓐ ${b}^{2}+7b-13=0$ ⓑ $5{a}^{2}-6a+10=0$ ⓒ $4{r}^{2}-20r+25=0$ ⓓ $7{t}^{2}-11t+3=0$

ⓐ ii ⓑ no real solutions ⓒ ane ⓓ 2

Identify the Most Appropriate Method to Use to Solve a Quadratic Equation

We have used four methods to solve quadratic equations:

Factoring
Square Root Belongings
Completing the Square
Quadratic Formula

You can solve any quadratic equation by using the Quadratic Formula, but that is not always the easiest method to employ.

Identify the almost appropriate method to solve a Quadratic Equation.

Try Factoring first. If the quadratic factors easily, this method is very quick.
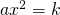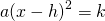Try the Square Root Property next. If the equation fits the form $a{x}^{2}=k$ or $a{\left(x-h\right)}^{2}=k$ , it can easily exist solved by using the Square Root Property.
Apply the Quadratic Formula. Whatsoever quadratic equation can be solved by using the Quadratic Formula.

What about the method of completing the foursquare? Most people find that method cumbersome and prefer not to utilise information technology. Nosotros needed to include it in this chapter because nosotros completed the square in general to derive the Quadratic Formula. You will also employ the process of completing the foursquare in other areas of algebra.

Identify the most advisable method to use to solve each quadratic equation:

ⓐ $5{z}^{2}=17$ ⓑ $4{x}^{2}-12x+9=0$ ⓒ $8{u}^{2}+6u=11$

Solution

ⓐ $5{z}^{2}=17$

Since the equation is in the $a{x}^{2}=k$ , the virtually appropriate method is to use the Square Root Property.

ⓑ $4{x}^{2}-12x+9=0$

We recognize that the left side of the equation is a perfect square trinomial, and then Factoring will be the most appropriate method.

Put the equation in standard form. $8{u}^{2}+6u-11=0$

While our outset thought may be to try Factoring, thinking about all the possibilities for trial and error leads us to cull the Quadratic Formula as the most appropriate method

Identify the most appropriate method to use to solve each quadratic equation:

ⓐ ${x}^{2}+6x+8=0$ ⓑ ${\left(n-3\right)}^{2}=16$ ⓒ $5{p}^{2}-6p=9$

ⓐ gene ⓑ Square Root Holding ⓒ Quadratic Formula

Identify the most advisable method to use to solve each quadratic equation:

ⓐ $8{a}^{2}+3a-9=0$ ⓑ $4{b}^{2}+4b+1=0$ ⓒ $5{c}^{2}=125$

ⓐ Quadratic Formula ⓑ factoring ⓒ Square Root Property

Key Concepts

Practice Makes Perfect

Solve Quadratic Equations Using the Quadratic Formula

In the following exercises, solve by using the Quadratic Formula.

$4{m}^{2}+m-3=0$

$m=-1,m=\frac{3}{4}$

$4{n}^{2}-9n+5=0$

$2{p}^{2}-7p+3=0$

$p=\frac{1}{2},p=3$

$3{q}^{2}+8q-3=0$

${p}^{2}+7p+12=0$

$p=-4,p=-3$

${q}^{2}+3q-18=0$

${r}^{2}-8r-33=0$

$r=-3,r=11$

${t}^{2}+13t+40=0$

$3{u}^{2}+7u-2=0$

$u=\frac{-7±\sqrt{73}}{6}$

$6{z}^{2}-9z+1=0$

$2{a}^{2}-6a+3=0$

$a=\frac{3±\sqrt{3}}{2}$

$5{b}^{2}+2b-4=0$

$2{x}^{2}+3x+9=0$

no real solution

$6{y}^{2}-5y+2=0$

$v\left(v+5\right)-10=0$

$v=\frac{-5±\sqrt{65}}{2}$

$3w\left(w-2\right)-8=0$

$\frac{1}{3}{m}^{2}+\frac{1}{12}m=\frac{1}{4}$

$m=-1,m=\frac{3}{4}$

$\frac{1}{3}{n}^{2}+n=-\frac{1}{2}$

$16{c}^{2}+24c+9=0$

$c=-\frac{3}{4}$

$25{d}^{2}-60d+36=0$

$5{m}^{2}+2m-7=0$

$m=-\frac{7}{5},m=1$

$8{n}^{2}-3n+3=0$

${p}^{2}-6p-27=0$

$p=-3,p=9$

$25{q}^{2}+30q+9=0$

$4{r}^{2}+3r-5=0$

$r=\frac{-3±\sqrt{89}}{8}$

$3t\left(t-2\right)=2$

$2{a}^{2}+12a+5=0$

$a=\frac{-6±\sqrt{26}}{2}$

$4{d}^{2}-7d+2=0$

$\frac{3}{4}{b}^{2}+\frac{1}{2}b=\frac{3}{8}$

$b=\frac{-2±\sqrt{11}}{6}$

$\frac{1}{9}{c}^{2}+\frac{2}{3}c=3$

$2{x}^{2}+12x-3=0$

$x=\frac{-6±\sqrt{42}}{4}$

$16{y}^{2}+8y+1=0$

Use the Discriminant to Predict the Number of Solutions of a Quadratic Equation

In the following exercises, make up one's mind the number of solutions to each quadratic equation.

Place the Most Advisable Method to Utilise to Solve a Quadratic Equation

In the following exercises, identify the almost appropriate method (Factoring, Foursquare Root, or Quadratic Formula) to apply to solve each quadratic equation. Do not solve.

Everyday Math

A flare is fired straight up from a ship at bounding main. Solve the equation $16\left({t}^{2}-13t+40\right)=0$ for $t$ , the number of seconds it volition take for the flare to be at an altitude of 640 anxiety.

five seconds, 8 seconds

An builder is designing a hotel lobby. She wants to accept a triangular window looking out to an atrium, with the width of the window 6 feet more than than the height. Due to energy restrictions, the surface area of the window must exist 140 foursquare feet. Solve the equation $\frac{1}{2}{h}^{2}+3h=140$ for $h$ , the height of the window.

Writing Exercises

Solve the equation ${x}^{2}+10x=200$
ⓐ past completing the square
ⓑ using the Quadratic Formula
ⓒ Which method do you prefer? Why?

Solve the equation $12{y}^{2}+23y=24$
ⓐ by completing the square
ⓑ using the Quadratic Formula
ⓒ Which method do you adopt? Why?

Self Bank check

ⓐ After completing the exercises, apply this checklist to evaluate your mastery of the objectives of this section.

This table has four rows and four columns. The first row is a header row and it labels each column. The first column is labeled "I can …", the second "Confidently", the third

ⓑ What does this checklist tell y'all about your mastery of this section? What steps will you take to improve?

trejocourester.blogspot.com

Source: https://opentextbc.ca/elementaryalgebraopenstax/chapter/solve-quadratic-equations-using-the-quadratic-formula/

What Are the Solutions to the Quadratic Equation (5y 6)2 = 24?

83 Solve Quadratic Equations Using the Quadratic Formula

Learning Objectives

Use the Discriminant to Predict the Number of Solutions of a Quadratic Equation

Identify the Most Appropriate Method to Use to Solve a Quadratic Equation

Key Concepts

Practice Makes Perfect

Everyday Math

Writing Exercises

Self Bank check

0 Response to "What Are the Solutions to the Quadratic Equation (5y 6)2 = 24?"

Enregistrer un commentaire

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel